The Amos Transformation
Amos Tversky was a cognitive psychologist and Daniel Kahneman’s research collaborator. Through their research, the two probed hypotheses of rationality that have broad implications in the field of behavioral economics. Among their many illusions of rationality, the one I find most compelling is the “asymmetry between the possibility effect and the certainty effect” (P. 315, Thinking Fast and Slow) that is a corollary of their famous Prospect Theory.
The possibility effect describes the tendency for highly unlikely outcomes (0-5%) to be weighted in our minds disproportionately more than their actual expected probability. On the opposite end of the spectrum, the certainty effect describes how we apply less weight to almost certain outcomes (95-100%) than what could be justified from their actual probability.
The operative word in these two descriptions is weight—or decision weight.
We all reflexively assign weights to particular characteristics when making a decision. Think about purchasing a house. You might consider the location to be paramount, while the kitchen layout less important. Or maybe price is all that matters even if This decision weight is the relationship between probability (expected value) and utility, where utility is defined as the usefulness of an outcome.
Say you were offered the following modest gamble proposition:
2% chance to win $100
50% chance to win $4
While a rational person would be quick to recognize these two options have the same expected value ($2), which one did you instinctively want more? What Tversky and Kahneman observed is that people do not conform to the rational model when presented propositions similar to the choice I proposed. They found that at the endpoints (0%, 100%) the weight assigned to the decision matched the corresponding probability as is predicted by the rational model (think about it, if you’re offered a 100% chance to win $10 or a 0% chance to win $1,000,000, which one would you choose? Obviously, the $10 guaranteed has more utility than nothing). But as soon as the probability emerges from these endpoints, rationality severely broke down.
Generally speaking, Tversky and Kahneman found that a 1% chance to gain had a decision weight 5.5x greater than the probability would suggest. Even a 10% real chance to gain was shown to have the same “utility” as an 18.6% outcome—this is the possibility effect. If a highly likely outcome is reduced from 100% to 99% (a 1% drop in probability), we tend to discount the utility of this outcome by 9%!—the certainty effect. At the midpoint this behavioral tendency is instructional: we only assign a 42% decision weight to a real 50/50 outcome!
Decision weights will vary depending on the application. Lawsuit settlements, insurance deductibles, stock option trading, and of course, gambling are just some applications where the discrepancy between real, underlying probabilities and their perceived utility influence decisions.
————
I don’t know the exact methods Vegas bookmakers deploy to set such sharp lines. I can reasonably infer that they use a combination of sophisticated models and aggregated data captured from their customers. As I’ve studied the art of bookmaking, I’ve grown strongly suspect there is an element of behavioral economics that influences their risk management.
Adding a behavioral element, I think, is the missing piece to building a prediction model that outperforms the consensus. This behavioral element is what I have named, “The Amos Transformation”, after the late, legendary behavioral psychologist.
Recognizing opportunity in the marketplace relies upon both the market environment and your model’s assessment to represent the true value of the element under consideration (whether that’s a new car, a potential stock investment, or sports wager). If the market reflects the true value of an element, your unbiased model (or your not-so-rational intuition) can judge whether this is an opportunity worth taking. Is this a fair price for this car? Will this stock go up in the timeframe I need? Will the Buccaneers win more than 9 games next season with Tom Brady? Usually, this is the environment we’re in and why unbiased models can help improve decisions.
However, what if the market doesn’t reflect the true value of a proposition? Say that house you want looks shoddy from the curb but you find that there’s a beautiful brick facade beneath the drywall; or that the public is so enamored with Brady and Gronk back together that their season win total has been overinflated to keep up with demand? In these situations, a model may still identify opportunity but it’s doing so against a false sense of reality. This is where the Amos Transformation comes into play.
Here’s how it works.
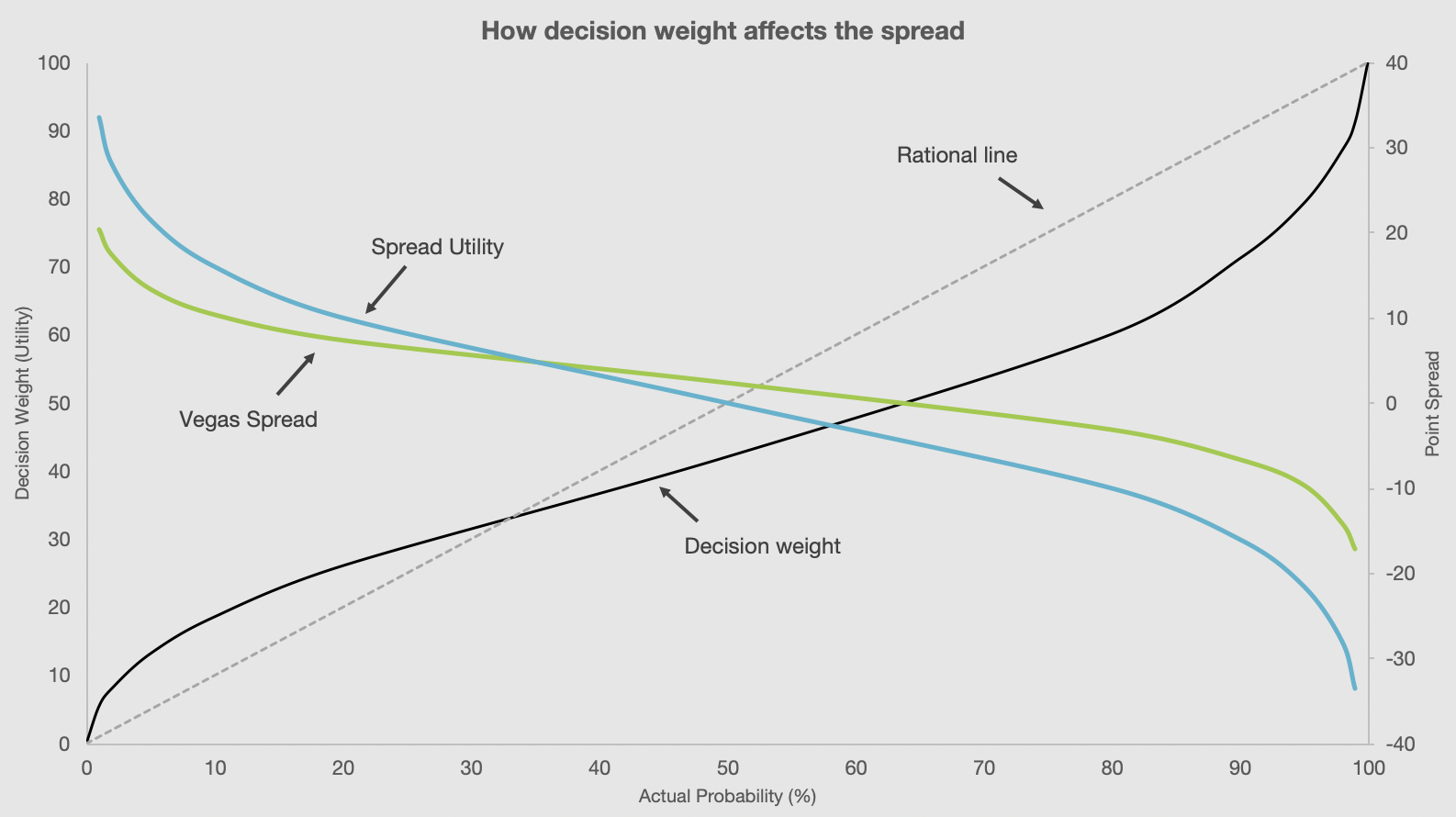
The plot below shows a generalized decision weight curve as a function of actual probability. As I noted above, a 50/50 outcome only has a decision weight of 42%. And while a 90% likely outcome only has the weight of 71%, a 2% likely outcome has a weight of 8%. Plotted on the secondary axis is the familiar football point spread (blue line) as a function of probability. That is, a spread of 0 is a 50/50 matchup, while a spread of -10 implies the favorite has a roughly 80% chance of winning.
Let’s see what happens when we replace the actual probability with its respective decision weight (the result shown as the green line). The hypothesis here is: Vegas exploits bettors’ tendencies to overweigh improbable outcomes and discount outcomes with a high likelihood. There are two ways to test this. The first is to build this transformation function into the model itself so the output can be easily compared to the market line. This makes the comparison back to the market line easier but it divorces the true probability from the model output, which can be confusing.
The method I prefer is to “transform” the Vegas line into its truer line. To do this, take the market line, find the utility that corresponds to the same probability and then determine what the point spread ought to be. For example, the more likely, “true” line in our +10 example is closer to +14.5. If you wanted to take the other side of the same game, a market line of -10 has a true value of -23. In both cases, the market line penalizes the bettor for their innate bias.
Now let’s apply this new way of analyzing the Vegas lines. Before I developed the Amos Transformation, a model suggestion of -15.5 when compared to a market line of -10 would lead one to bet the favorite. Applying the Amos Transformation now identifies -10 as really equivalent to -23 and the model suggestion of -15.5 points towards the taking the underdog—even if the raw -10 appears on its face to show value. You’ll notice the transformation isn’t symmetric. This is because we are loss adverse and desire a slight premium to wager on a 50/50 proposition.
More refinement needs to be done to optimize the curve and even apply team/sport specific transforms. The Amos Transformation is straight from the latest thinking from this blog. Just another way to improve and differentiate model performance.